PERCOBAAN 2
SISTEM DENGAN JARINGAN RADIAL
A. TUJUAN
Mahasiswa dapat menganalisa sistem radial dengan program matlab.
B. DASAR TEORI
- Diagram Satu Garis
Sistem tenaga merupakan rangkaian listrik yang rumit. Disamping banyaknya macam piranti yang ada di dalamnya, sistem ini juga sistem multifasa (umumnya tiga-fasa), dan ia beroperasi pada banyak tingkat tegangan. Agar analisis dapat dilakukan, maka sistem tenaga harus dapat dinyatakan secara mudah.
Langkah pertama dalam analisis adalah memindahkan rangkaian sistem tenaga ke atas kertas dalam bentuk diagram rangkaian. Diagram rangkaian untuk sistem tenaga berupa diagram satu garis (single line diagram). Diagram ini sederhana namun menunjukkan secara lengkap interkoneksi berbagai piranti. Walaupun hanya satu garis, ia menggambarkan sistem multifasa. Berikut ini contoh dari diagram satu garis.
Gambar di atas, memperlihatkan sebuah generator terhubung Y, dengan titik netral yang ditanahkan melalui sebuah impedansi. Generator ini dihubungkan ke trasformator tiga belitan melalui bus-1. Belitan primer trafo terhubung ∆, belitan sekunder terhubung Y dengan titik netral ditanahkan langsung dan terhubung ke bus-2, sedangkan belitan tertier dihubungkan ∆masuk ke bus-3 untuk mencatu beban.
Dari bus-2 melalui circuit breakermasuk ke saluran transmisi melalui bus-4. Ujung saluran transmisi melalui bus-5 terhubung ke transformator 2 belitan; transformator ini terhubung Y-∆dengan titik netral primernya ditanahkan langsung. Sekunder transformator terhubung ke bus-6 untuk mencatu beban.
Dalam diagram satu garis, impedansi-impedansi tidak digambarkan. Untuk analisis, diagram satu garis perlu “diterjemahkan” menjadi diagram rangkaian listrik model satu fasa seperti terlihat pada gambar di bawah.
Dengan model satu fasa inilah analisis dilakukan. Dalam gambar ini saluran transmisi dinyatakan dengan rangkaian ekivalennya, yaitu rangkaian ekivalen π.
- Sistem Per-Unit
Sistem per-unit sesungguhnya merupakan cara penskalaan atau normalisasi. Besaran-besaran sistem dalam satuan masing-masing, tegangan dalam volt – arus dalam ampere – impedansi dalam ohm, ditransformasikan ke dalam besaran tak berdimensi yaitu per-unit (disingkat pu). Pada mulanya transformasi ke dalam per-unit dimaksudkan untuk mempermudah perhitungan, namun dengan perkembangan penggunaan computer maksud penyederhanaan itu sudah kurang berarti lagi. Walaupun demikian, beberapa keuntungan yang terkandung dalam sistem per-unit (yang akan kita lihat kemudian) masih terasakan dan oleh karena itu kita akan pelajari.
Nilai per-unit dari suatu besaran merupakan rasio dari besaran tersebut dengan suatu besaran basis. Besaran basis ini berdimensi sama dengan dimensi besaran aslinya sehingga nilai per-unit besaran itu menjadi tidak berdimensi
Nilai sesungguhnya mungkin berupa bilangan kompleks, namun nilai basis yang ditetapkan adalah bilangan nyata. Oleh karena itu sudut fasa nilai dalam per-unit sama dengan sudut fasa sesungguhnya. Sebagai contoh kita ambil daya kompleks
di mana αadalah sudut fasa tegangan dan βadalah sudut fasa arus. Untuk menyatakan S dalam per-unit kita tetapkan S basis yang berupa bilangan nyata, sehingga
Nilai Sbasis dipilih secara bebas dan biasanya dipilih angka yang memberi kemudahan seperti puluhan, ratusan dan ribuan. Jika Sbasis sudah ditentukan kita harus memilih salah satu Vbasis atau Ibasis untuk ditentukan secara bebas, tetapi tidak kedua-duanya bisa dipilih bebas. Jika kita hitung Spu dari persamaan di atas kita peroleh
Nilai basis untuk impedansi ditentukan menggunakan relasi
Dengan Zbasis ini relasi arus dan tegangan V=Z.I atau Z=V/I akan memberikan
Karena Z = R + jX maka,
Jadi tidaklah perlu menentukan nilai basis untuk R dan X secara sendiri-sendiri. Selain itu tidak pula diperlukan menentukan nilai basis untu P dan Q secara sendiri-sendiri pula.
Setelah dilakukan penskalaan menjadi per unit, sistem baru bisa dihitung load flownya.
C. ALAT BAHAN
- Komputer / laptop
- Software Matlab
D. LANGKAH PERCOBAAN
1. Sistem tanpa trafo
Simulasikan rangkaian di bawah dengan matlab, hitung nilai arus yang mengalir ke beban juga hitung tegangannya.
Simulasikan juga dengan software selain matlab, bandingkan nilainya.
Gunakan base tegangan 13 kV, Power base 10 MVA.
Rubah nilai beban menjadi 300 + j200 Ohm
Simulasikan dengan matlab, hitung nilai arus dan tegangan beban
Tambahkan kapasitor agar daya reaktif bisa dikurangi.
Simulasikan juga dengan software selain matlab.
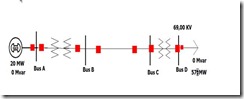
2. Sistem dengan trafo
Simulasikan rangkaian di bawah dengan matlab, hitung nilai arus yang mengalir ke beban juga hitung tegangannya.
Simulasikan juga dengan software selain matlab, bandingkan nilainya.
Rubah nilai beban menjadi 300 + j200 Ohm
Simulasikan dengan matlab, hitung nilai arus dan tegangan beban
Tambahkan kapasitor agar daya reaktif bisa dikurangi.
Simulasikan juga dengan software selain matlab.
Simulasikan jika terjadi short circuit di beban.
3. Sistem dengan beban motor
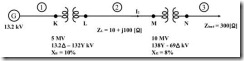
Sebuah generator fasa tiga 20 kV, 300 MVA mempunyai reaktansi sub-peralihan
sebesar 20%. Generator itu mencatu beberapa motor serempak melalui saluran transmisi
sepanjang 64 km (40 mil) yang mempunyai transformator pada kedua ujungnya, seperti
diperlihatkan pada diagram segaris dari Gambar 8.5. Motor yang semuanya mempunyai
rating 13,2 kV, dilukiskan sebagai dua buah motor ekivalen saja. Netral dari salah satu motor tersebut, M1, dihubungkan ke tanah melalui reaktansi. Netral dari motor kedua, M2, tidak dihubungkan ke tanah (suatu keadaan yang tidak biasa). Masukan nominal untuk M1 dan M2 berturut-turut adalah 200 MVA dan 100 MVA. Untuk kedua motor itu X" = 20%. Transformator fasa tiga T1 mempunyai rating 350 MVA, 230/20 kV dengan reaktansi bocor sebesar 10%. Transformator T2 terdiri atas tiga buah transformator fasa tunggal masing-masing dengan rating 127/13,2 kV, 100 MVA dengan reaktansi bocor sebesar 10%. Reaktansi seri saluran transmisi adalah 0,5 /km. Gambarlah diagram reaktansi dengan memilih rating generator sebagai dasar pada rangkaian generator.
Simulasikan dengan matlab / power world, hitung nilai arus dan tegangan beban
E. HASIL PERCOBAAN
1. Sistem tanpa trafo
1. Beban 300 ohm
sb=10000000
v1b=13800
zload=300
zline=10+10j
z3b = (v1b^2)/sb
zb=zload/z3b
z2b= (v1b^2)/sb
zln=zline/z2b
ztotal=zb+zln
ztotals=sqrt(10^2+10^2)
Es=13/13
Ipu=Es/ztotals
v3pu=zb*Ipu
v3=v3pu*13
hasil
sb =
10000000
v1b =
13800
zload =
300
zline =
10.0000 +10.0000i
z3b =
19.0440
zb =
15.7530
z2b =
19.0440
zln =
0.5251 + 0.5251i
ztotal =
16.2781 + 0.5251i
ztotals =
14.1421
Es =
1
Ipu =
0.0707
v3pu =
1.1139
v3 =
14.4808
2. Beban 300+j200
sb=10000000
v1b=13800
zload=300+200j
zline=10+10j
z3b = (v1b^2)/sb
zb=zload/z3b
z2b= (v1b^2)/sb
zln=zline/z2b
ztotal=zb+zln
ztotals=sqrt(10^2+10^2)
Es=13/13
Ipu=Es/ztotals
v3pu=zb*Ipu
v3=v3pu*13
Hasilnya..
sb =
10000000
v1b =
13800
zload =
3.0000e+002 +2.0000e+002i
zline =
10.0000 +10.0000i
z3b =
19.0440
zb =
15.7530 +10.5020i
z2b =
19.0440
zln =
0.5251 + 0.5251i
ztotal =
16.2781 +11.0271i
ztotals =
14.1421
Es =
1
Ipu =
0.0707
v3pu =
1.1139 + 0.7426i
v3 =
14.4808 + 9.6538i
2. Sistem dengan trafo
A. HASIL PERHITUNGAN MATLAB BEBAN 300 OHM
SB = 10000000
SBT1 = 5000000
SBT2 = 10000000
V3B = 69000
V2B = 138000
V1B = 13200
VG = 13200
VB = 13800
X11 = 0,1
X12 = 0,08
ZL = 10+10j
Zbeban = 300
Z3B = (V3B)^2/SB
ZLOAD = Zbeban/Z3B
Z2B = (V2B)^2/SB
ZLINE = ZL/Z2B
XT1 = 0,1*((VG/VB)^2)*(10000000/5000000)
XT2 = 0.08*((VG/VB)^2)*(SB/SBT1)
ZTOTAL = ZLOAD+ZLINE+1.8299+0.1464
ES = 13200/13800
Ipu = ES/2,6117
V3pu = ZLOAD*Ipu
V3 = V3pu*69
HASILNYA:
SB =
10000000
SBT1 =
5000000
SBT2 =
10000000
V3B =
69000
V2B =
138000
V1B =
13200
VG =
13200
VB =
13800
X11 =
0
ans =
1
X12 =
0
ans =
8
ZL =
10.0000 +10.0000i
Zbeban =
300
Z3B =
476.1000
ZLOAD =
0.6301
Z2B =
1.9044e+003
ZLINE =
0.0053 + 0.0053i
XT1 =
0
ans =
1.8299
XT2 =
0.1464
ZTOTAL =
2.6117 + 0.0053i
ES =
0.9565
Ipu =
0.4783
ans =
6117
V3pu =
0.3014
V3 =
20.7940
B. HASIL PERHITUNGAN MATLAB BEBAN 300+J200 OHM
SB = 10000000
SBT1 = 5000000
SBT2 = 10000000
V3B = 69000
V2B = 138000
V1B = 13200
VG = 13200
VB = 13800
X11 = 0,1
X12 = 0,08
ZL = 10+10j
Zbeban = 300+200j
Z3B = (V3B)^2/SB
ZLOAD = Zbeban/Z3B
Z2B = (V2B)^2/SB
ZLINE = ZL/Z2B
XT1 = 0,1*((VG/VB)^2)*(10000000/5000000)
XT2 = 0.08*((VG/VB)^2)*(SB/SBT1)
ZTOTAL = ZLOAD+ZLINE+1.8299+0.1464
ES = 13200/13800
Ipu = ES/2,6117
V3pu = ZLOAD*Ipu
V3 = V3pu*69
HASIL:
SB =
10000000
SBT1 =
5000000
SBT2 =
10000000
V3B =
69000
V2B =
138000
V1B =
13200
VG =
13200
VB =
13800
X11 =
0
ans =
1
X12 =
0
ans =
8
ZL =
10.0000 +10.0000i
Zbeban =
3.0000e+002 +2.0000e+002i
Z3B =
476.1000
ZLOAD =
0.6301 + 0.4201i
Z2B =
1.9044e+003
ZLINE =
0.0053 + 0.0053i
XT1 =
0
ans =
1.8299
XT2=
0.1464
ZTOTAL =
2.6117 + 0.4253i
ES =
0.9565
Ipu =
0.4783
ans =
6117
V3pu =
0.3014 + 0.2009i
V3 =
20.7940 +13.8626i
3. Sistem dengan beban motor
PERHITUNGAN MATLAB
VT = 13.2/((sqrt(3))*127)*230
XT1 = 0.1*((20/20)^2)*(300/350)
XT2 = 0.1*((13.2/13.8)^2)*(300/300)
XG = 0.2*((20/20)^2)*(300/300)
Z2B = (0.230/300)^2
ZLINE = 32/176.3
%BEBAN PARALEL
% 1/XM12 = 1/XM1 + 1/XM2
XM12 = 1/5,47
ZTOTAL = XG+XT1+XT2+ZLINE+XM12
ES = 20/20
Ipu = ES/0.741
V3pu = 0.8128*Ipu
V3 = V3pu*13.2
HASIL
VT =
13.8019
XT1 =
0.2745
XT2 =
0.5490
XG =
0.2000
Z2B =
5.8778e-007
VT =
13.8019
XT1 =
0.2745
XT2 =
0.5490
XG =
0.2000
Z2B =
5.8778e-007
ZLINE =
5.4442e+007
VT =
13.8019
XT1 =
0.2745
XT2 =
0.5490
XG =
0.2000
Z2B =
5.8778e-007
ZLINE =
0.1815
VT =
13.8019
XT1 =
0.0857
XT2 =
0.0915
XG =
0.2000
Z2B =
5.8778e-007
ZLINE =
0.1815
XM12 =
0.2000
ans =
47
ZTOTAL =
0.7587
ES =
1
Ipu =
1.3495
V3pu =
1.0969
V3 =
14.4790





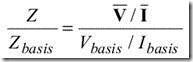



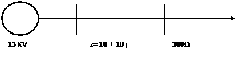



Tidak ada komentar:
Posting Komentar