Jobsheet Praktikum Pengukuran Listrik Menggunakan Amperemeter dan Voltmeter

JOBSHEET PRAKTIKUM PENGUKURAN LISTRIK MENGGUNAKAN

AMPEREMETER DAN VOLTMETER

 

I. TUJUAN

1. Mengenal alat ukur yang digunakan dalam pekerjaan instalasi listrik

2. Mengetahui cara pengukuran listrik menggunakan Ampermeter dan Voltmeter

3. Mengetahui prinsip kerja alat ukur Ampermeter dan Voltmeter

4. Menggunakan Amperemeter dan Voltmeter dalam rangkaian listrik

 

II. DASAR TEORI

1. Amperemeter

Amperemeter adalah alat yang digunakan untuk mengukur kuat arus listrik. Umumnya alat ini dipakai oleh teknisi elektronik dalam alat multi tester listrik yang disebut avometer gabungan dari fungsi amperemeter, voltmeter dan ohmmeter. Amper meter dapat dibuat atas susunan mikroamperemeter dan shunt yang berfungsi untuk deteksi arus pada rangkaian baik arus yang kecil, sedangkan untuk arus yang besar ditambhan dengan hambatan shunt. Amperemeter bekerja sesuai dengan gaya lorentz gaya magnetis. Arus yang mengalir pada kumparan yang selimuti medan magnet akan menimbulkan gaya lorentz yang dapat menggerakkan jarum amperemeter. Semakin besar arus yang mengalir maka semakin besar pula simpangannya.

a. Gambar Amperemeter

Amperemeter bekerja berdasarkan prinsip gaya magnetik (Gaya Lorentz). Ketika arus mengalir melalui kumparan yang dilingkupi oleh medan magnet timbul gaya lorentz yang menggerakan jarum penunjuk menyimpang. Apabila arus yang melewati kumparan besar, maka gaya yang timbul juga akan membesar sedemikian sehingga penyimpangan jarum penunjuk juga akan lebih besar. Demikian sebaliknya, ketika kuat arus tidak ada maka jarum penunjuk akan dikembalikan ke posisi semula oleh pegas. Besar gaya yang dimaksud sesuai dengan Prinsip gaya Lorentz F = B.I.L. Kuat arus yang terukur I dapat dihitung dengan rumus :

Cara pengukuran menggunakan Amperemeter :

b. Cara penggunaan Amperemeter

2. Voltmeter

Voltmeter adalah suatu alat yang berfungsi untuk mengukur tegangan listrik. Dengan ditambah alat multiplier akan dapat meningkatkan kemampuan pengukuran alat voltmeter berkali-kali lipat. Gaya magnetik akan timbul dari interaksi antar medan magnet dan kuat arus. Gaya magnetic tersebut akan mampu membuat jarum alat pengukur voltmeter bergerak saat ada arus listrik. Semakin besar arus listrik yang mengelir maka semakin besar penyimpangan jarum yang terjadi.

c. Gambar Voltmeter

Prinsip Kerja Voltmeter hampir sama dengan Amperemeter karena desainnya juga terdiri dari galvanometer dan hambatan seri atau multiplier. Galvanometer menggunakan prinsip hukum Lorentz, dimana interaksi antara medan magnet dan kuat arus akan menimbulkan gaya magnetic. Gaya magnetik inilah yang menggerakan jarum penunjuk sehingga menyimpang saat dilewati oleh arus yang melewati kumparan. Makin besar kuat arus akan makin besar penyimpangannya.

Untuk mengukur tegangan kita harus menggunakan voltmeter yang dipasang paralel terhadap komponen yang kita ukur beda potensialnya. Jadi tidak perlu dilakukan pemutusan penghantar seperti pada amperemeter Pada rangkaian arus searah pemasangan kutub-kutub voltmeter harus sesuai. Kutub positip dengan potensial tinggi dan kutub negatip dengan potensial rendah. Biasanya ditandai dengan kabel yang berwarna hitam dan merah atau biru. Bila pemasangan terbalik akan terlihat penyimpangan yang arahnya ke kiri. Sedangkan pada rangkaian arus bolak balik tidak menjadi masalah. Setelah voltmeter terpasang dengan benar maka hasil pengukuran harus memperhatikan bagaimana menuliskan hasil pengukuran yang benar. Tegangan yang terukur (V) adalah:

Cara pengukuran menggunakan Voltmeter:

d. Cara penggunaan Voltmeter

III. Alat dan Bahan

1. Voltmeter 1 buah

2. Amperemeter 1 buah

3. Lampu Pijar 40W/220V 1 buah

4. Lampu Pijar 60W/220V 1 buah

5. Lampu Pijar 100W/220V 1 buah

6. Kabel 1,5 mm secukupnya

7. Fiting duduk 3 buah

8. Kabel steker 1 buah

9. Saklar tunggal 3 buah

10. Tang potong 1 buah

IV. Keselamatan dan Kesehatan Kerja

1. Gunakan pakaian praktik

2. Bacalah dan pahami petunjuk praktikum pada setiap lembar kegiatan.

3. Jangan meletakkan alat dan bahan praktikum ditepi meja dan didekat dengan sumber tegangan listrik.

4. Jangan bergurau pada waktu melakukan praktik.

5. Lakukan pengamatan dan pengukuran dengan teliti.

6. Hati-hati melakukan praktik.

V. Langkah Kerja

1. Siapkan alat dan bahan yang digunakan dalam praktik

2. Rangkailah alat dan bahan sesuai dengan gambar.

3. Periksa kembali rangkaian, apakah sudah benar.

4. Lakukan pengukuran dengan langkah-langkah sebagai berikut:

a. Nyalakan lampu 1 dengan saklar 1, dan catat hasil pengukuran pada table.

b. Matikan lampu 1 dan nyalakan lampu 3 dengan saklar 2 dan catat hasil pengukurannya.

c. Matikan lampu 2 dan nyalakan lampu 3 dengan saklar 3, catat hasil pengukurannya.

5. Masukkan data-data tersebut dan hitunglah daya masing-masing lampu dengan menggunakan rumus W = E x I

6. Hentikan kegiatan dan kembalikan semua peralatan ketempat semula.

Gambar Bagan

VI. HASIL

VII. PENUGASAN

1. Buat kesimpulan dari hasil praktikum

2. Setelah melakukan pratik, buat laporan praktikum pengukuran listrik.

PRAKTIKUM MATLAB

LAPORAN 1

PRAKTIKUM MATLAB

Untuk Memenuhi Tugas Praktikum Sistem Tenaga Listrik

Oleh:

Mohammad Rizza

120534431451

S1 PTE AJ 2012

PROGRAM STUDI S1 PENDIDIKAN TEKNIK ELEKTRO

JURUSAN ELEKTRO FAKULTAS TEKNIK

UNIVERSITAS NEGERI MALANG

2012

 

PERCOBAAN 1

MENGENAL SINTAK-SINTAK PEMROGRAMAN DI MATLAB

Tujuan

Agar mahasiswa dapat mengetahui sintak-sintak yang ada pada matlab yang akan digunakan sebagai perhitungan analisa sitem tenaga listrik.

Dasar Teori

Matlab merupakan MATLAB (Matrix Laboratory) adalah bahasa tingkat tinggi dan interaktif yang memungkinkan untuk melakukan komputasi secara intensif. MATLAB telah berkembang menjadi sebuah environment pemrograman yang canggih yang berisi fungsi-fungsi built-in untuk melakukan pengelolahan sinyal, aljabar linear dan kalkulasi matematis lainnya. MATLAB juga berisi toolbox yang berisi fungsi-fungsi tambahan untuk aplikasi khusus. Penggunaan MATLAB meliputi bidangbidang: Matematika, komputasi, pembentukan algoritma, akuisi data, pemodelan, prototype, simulasi, analisis data, exsplorasi, visualisasi, grafik keilmuan dan bidang rekayasa.

Matlab dikembangkan oleh MathWorks, yang pada awalnya dibuat untuk memberikan kemudahan mengakses data matrik pada proyek LINPACK dan EISPACK. Saat ini matlab memiliki ratusan fungsi yang dapat digunakan sebagai problem solver mulai dari simple sampai masalah-masalah yang kompleks dari berbagai disiplin ilmu.

· Current Directory

Window ini menampilkan isi dari direktori kerja saat menggunakan matlab. Kita dapat mengganti direktori ini sesuai dengan tempat direktori kerja yang diinginkan. Default dari alamat direktori berada dalam folder works tempat program files Matlab berada.

· Command History

Window ini berfungsi untuk menyimpan perintah-perintah apa saja yang sebelumnya dilakukan oleh pengguna terhadap matlab.

· Command Window

Window ini adalah window utama dari Matlab. Disini adalah tempat untuk menjalankan fungsi, mendeklarasikan variable, menjalankan proses-proses , serta melihat isi variable.

· Workspace

Workspace berfungsi untuk menampilkan seluruh variabel-variabel yang sedang aktif pada saat pemakaian matlab. Apabila variabel berupa data matriks berukuran besar maka user dapat melihat isi dari seluruh data dengan melakukan double klik pada variabel tersebut. Matlab secara otomatis akan menampilkan window “array editor” yang berisikan data pada setiap variabel yang dipilih user.

Gambar berikut menampilkan tampilan antar muka dari matlab versi 7.0.

Alat Bahan

- Komputer / Laptop

- Software Matlab

- Modul Practical Matlab for Engineers

Langkah Percobaan

1. Instal matleb pada PC/Laptop

2. Buka matleb yang sudah terinstal dengan baik

3. Klik file new serta M-file pada Matlab untuk membuat halaman baru

4. Simpan halaman baru yang sudah terisi tugas yang akan digunakan

5. Setelah itu klik tool dan ran

A. Menyelesaikan Persamaan Matematika Dasar

Tugas 1

Tugas 2

Mencari akar persamaan dari:

Tugas 3 (menggunakan fungsi)

Mencari akar persamaan dari dengan operator:

(Untuk seterusnya lihat di buku Practical Matlab for Engineers bab 2)

Percobaan B, Menyelesaikan Matrik Dan Vektor

· Penjumlahan pengurangan matrik

· Perkalian pembagian matrik

(Lihat di buku Practical Matlab for Engineers bab 3)

Percobaan C, Trigonometric, Exponential, Logarithmic, And Special Functions

(Lihat di buku Practical Matlab for Engineers bab 4)

Percobaan D, Printing & Ploting

(Lihat di buku Practical Matlab for Engineers bab 5)

Percobaan E, Operasi Bilangan Komplek

(Lihat di buku Practical Matlab for Engineers bab 6)

HASIL PERCOBAAN

A. Penyelesaian Perhitungan Matematika Sederhana

Tugas 1

Hasil perhitungan di matlab

x = 4+2^3-sqrt(4^2-7)/(2^2)*4^2-1

x =

-5

y = 1+(3^2-4)^2/(sqrt(2^4+9)+5)*2^3

y =

21

Tugas 2

Solusi di matlab

a = 1

b = 2

c = 3

root1 = (-b+sqrt(b^2-4*a*c))/(2*a)

root2 = (-b-sqrt(b^2-4*a*c))/(2*a)

hasil

latihan4

a =

1

b =

2

c =

3

root1 =

-1.0000 + 1.4142i

root2 =

-1.0000 - 1.4142i

Tugas 3

Solusi matlab

a. 2x² + 3x + 7 = 0

a = 2

b = 3

c = 7

root1 = (-b+sqrt(b^2-4*a*c))/(2*a)

root2 = (-b-sqrt(b^2-4*a*c))/(2*a)

hasil

a =

2

b =

3

c =

7

root1 =

-0.7500 + 1.7139i

root2 =

-0.7500 - 1.7139i

b. πx² + 2 πx + 3 π = 0

a = pi

b = 2*pi

c = 3*pi

root1 = (-b+sqrt(b^2-4*a*c))/(2*a)

root2 = (-b-sqrt(b^2-4*a*c))/(2*a)

hasil

a =

3.1416

b =

6.2832

c =

9.4248

root1 =

-1.0000 + 1.4142i

root2 =

-1.0000 - 1.4142i

c. log10(32.3)x2 + sqrt(3^3 + 1.33^3.3)x + tan(1.112) = 0

a = log10(32.3)

b = sqrt (3^3+1.33^3.3)

c = tan (1.112)

root1 = (-b+sqrt(b^2-4*a*c))/(2*a)

root2 = (-b-sqrt(b^2-4*a*c))/(2*a)

hasil

a =

1.5092

b =

5.4372

c =

2.0245

root1 =

-0.4217

root2 =

-3.1810

d. P =7300;

I =2.7;

n =5;

format bank

Total_amount = P*(1+I/100)^n

Hasil

Total_amount =

8340.17

B. Percobaan B, Menyelesaikan Matrik Dan Vektor

1. A = [1 2; 3 4]

hasil

A =

1 2

3 4

2. A = [1 2;3 4;5 6];

size(A)

Hasil

A =

1 2

3 4

ans =

3 2

3. A = [1 2 3]

B = [1;2;3]

Hasil

A =

1 2 3

B =

1

2

3

4. n = 2:-0.1:1

hasil

n =

Columns 1 through 7

2.0000 1.9000 1.8000 1.7000 1.6000 1.5000 1.4000

Columns 8 through 11

1.3000 1.2000 1.1000 1.0000

5. u = [0 1]

v = [2 3]

# s = [u v]

hasil

u =

0 1

v =

2 3

s =

0 1 2 3

# ss = [u;v]

ss =

0 1

2 3

# sss = [ss,ss;ss,ss]

sss =

0 1 0 1

2 3 2 3

0 1 0 1

2 3 2 3

6. X = [2*pi:pi/3:3*pi;3*pi:pi/3:4*pi

Y = log(X

Hasil

X =

6.2832 7.3304 8.3776 9.4248

9.4248 10.4720 11.5192 12.5664

Y =

1.8379 1.9920 2.1256 2.2433

2.2433 2.3487 2.4440 2.5310

7. A = [2 -3 5;6 -9 7]

B = [4 5;-3 1;6 -9]

C = A*B dan D = B*A

Hasil

A =

2 -3 5

6 -9 7

B =

4 5

-3 1

6 -9

C =

47 -38

93 -42

D =

38 -57 55

0 0 -8

-42 63 -33

8. A = [3 0 0; 0 2 0; 0 0 1]

B = [1 4 7;2 5 8;3 6 -9]

a. cond(A) rcond(A)]

b. det(B)

c. [cond(B) rcond(B) 1/rcond(B)]

Hasil

A =

3 0 0

0 2 0

0 0 1

B =

1 4 7

2 5 8

3 6 -9

a. ans = 3.0000 0.4490

b. ans = 54

c. ans = 34.2158 0.0185 54.1818

9. A = [1 2 1; 2 -1 1; 4 2 5];

B = [0; 5; 6];

a. Solution_A = inv(A)*B

b. Solution_B =A\B

c. C = [A B];

Gauss = rref (C);

Solution_C = Gauss(:,4)

Hasil

a. Solution_A =

2.0000

-1.0000

0

b. Solution_B =

2

-1

0

c. Solution_C =

2

-1

0

10. calendar ('05/05/1941')

hasil

matrik10

May 1941

S M Tu W Th F S

0 0 0 0 1 2 3

4 5 6 7 8 9 10

11 12 13 14 15 16 17

18 19 20 21 22 23 24

25 26 27 28 29 30 31

0 0 0 0 0 0 0

11. A = [1 3 0; 4 8 2; 3 -1 -1];

B = [1 6 5.3; 1.8 7 3; 2 5 0];

a. C = A+B

b. D = A-B

c. E = A.*B

d. F = A./B

e. A2 = A(:, 2)

f. B1 = B(:, 1)

g. G = A2+B1

h. cond(A)

hasil

a. C =

2.0000 9.0000 5.3000

5.8000 15.0000 5.0000

5.0000 4.0000 -1.0000

b. D =

0 -3.0000 -5.3000

2.2000 1.0000 -1.0000

1.0000 -6.0000 -1.0000

c. E =

1.0000 18.0000 0

7.2000 56.0000 6.0000

6.0000 -5.0000 0

Warning: Divide by zero.

> In C:\MATLABR11\work\matrik11.m at line 6

d. F =

1.0000 0.5000 0

2.2222 1.1429 0.6667

1.5000 -0.2000 -Inf

e. A2 =

3

8

-1

f. B1 =

1.0000

1.8000

2.0000

g. G =

4.0000

9.8000

1.0000

h. ans =

12.9106

C. Trigonometric, Exponential, Logarithmic, And Special Functions

1. rat(pi)

ans =3 + 1/(7 + 1/(16))

[N,D] = rat(pi)

N =355

D =113

[N,D] = rat(exp(1))

N =1457

D =536

check = 1457/536

check =2.7183

HASIL :

N =

1457

D =

536

check =

2.7183

check =

2.7183

2. n =1:1:10;

den = cumprod(n);

series = cumsum(1./den);

exposeri = 1+series

den1 = 1./n;

exp = (1 +den1).^n;

HASIL :

exposeri =

Columns 1 through 7

2.0000 2.5000 2.6667 2.7083 2.7167 2.7181 2.7183

Columns 8 through 10

2.7183 2.7183 2.7183

3. a = [30 15 15 30];b=[90 90];

increm = [0 a a b];

angle_deg = cumsum(increm)

convert = ones(1,11)*pi/180;

angle_rad = angle_deg.*convert;

sinx = sin(angle_rad);

cosx = cos(angle_rad);

HASIL :

angle_deg =

0 30 45 60 90 120 135 150 180 270 360

D. Printing & Ploting

1. display the values of x = 1, π, and e.

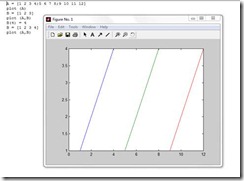
2. Grafik Differensial

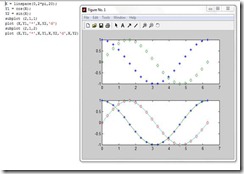
3. Plot grafik sin dan cos

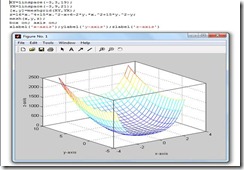
4. Ploat Matriks

E. Operasi Bilangan Komplek

Bilangan complex

1. X= [-2:0.05: 8];

Y1 = X.^2-6*X-7;

Y2 = X.^2-6*X+9;

Y3 = X.^2-6*X+10;

subplot(3,1,1)

plot (X,Y1)

axis on, grid on

xlabel(X), ylabel(Y1)

subplot(3,1,2)

plot (X,Y2)

axis on, grid on

xlabel(X), ylabel(Y2)

subplot(3,1,3)

plot (X,Y3)

hasil

2. axis on, grid on

xlabel(X), ylabel(Y3)

P1 = [1 -6 -7];

P2 = [1 -6 9];

P3 = [1 -6 10];

roots(P1)

hasil

ans =

7

-1

3. axis on, grid on

xlabel(X), ylabel(Y3)

P1 = [1 -6 -7];

P2 = [1 -6 9];

P3 = [1 -6 10];

roots(P2)

hasil

ans =

3

3

4. axis on, grid on

xlabel(X), ylabel(Y3)

P1 = [1 -6 -7];

P2 = [1 -6 9];

P3 = [1 -6 10];

roots(P3)

hasil

ans =

3.0000 + 1.0000i

3.0000 - 1.0000i

5. sqrt(-1)

hasil

ans =

0 + 1.0000i

6. a = 1:2:11;

b = 2:2:12

sequence = (complex(a,b))

hasil

b =

2 4 6 8 10 12

sequence =

Columns 1 through 4

1.0000 + 2.0000i 3.0000 + 4.0000i 5.0000 + 6.0000i 7.0000 + 8.0000i

Columns 5 through 6

9.0000 +10.0000i 11.0000 +12.0000i

7. z =1+2i;

C1 =1+z*exp(z)

C2 = 3-z^2+1/z*log10(z)

Hasil

C1 =

-5.0747 + 0.2093i

C2 =

6.2622 - 4.0436i

8. x = (-1)^(1/5)

y = x^5

X= [1 0 0 0 0 1];

Hasil

x =

0.8090 + 0.5878i

y =

-1.0000

9. y = log(3+4i)

z = exp(y)

Hasil

y =

1.6094 + 0.9273i

z =

3.0000 + 4.0000i

10. z1 = 8+10i

z2 = 3-9i

z3 = 5-12j

z4 = 7-i*13

Sum = z1+z2

Prod = z1*z2

Div =z1/z2

w = z1*z2+z3*z4

v = z1^2+z2^2+z3^2+z4^2

hasil

z1 =

8.0000 +10.0000i

z2 =

3.0000 - 9.0000i

z3 =

5.0000 -12.0000i

z4 =

7.0000 -13.0000i

Sum =

11.0000 + 1.0000i

Prod =

1.1400e+002 -4.2000e+001i

Div =

-0.7333 + 1.1333i

w =

-7.0000e+000 -1.9100e+002i

v =

-3.4700e+002 -1.9600e+002i

11. A = [3*exp(pi/3*j) 6*cos(pi/6)+i*6*sin(pi/6);3+4i 4.23*exp(-i*pi/18)+9]

B = [5-9j 5*exp(pi/3*j+pi/5);(2-3j)^3.3 log(6-8j)]

C = A+B

D = A*B

E = A.*B

F = inv(A)

G = F*A

H = A*F

I = A^i

J = A.^B

Hasil

A =

1.5000 + 2.5981i 5.1962 + 3.0000i

3.0000 + 4.0000i 13.1657 - 0.7345i

B =

5.0000 - 9.0000i 4.6861 + 8.1166i

-68.5109 + 6.9866i 2.3026 - 0.9273i

C =

6.5000 - 6.4019i 9.8823 +11.1166i

-65.5109 +10.9866i 15.4683 - 1.6618i

D =

1.0e+002 *

-3.4607 - 1.6974i 0.0069 + 0.2644i

-8.4587 + 1.3531i 0.1123 + 0.2919i

E =

1.0e+002 *

0.3088 - 0.0051i 0.0000 + 0.5623i

-2.3348 - 2.5308i 0.2963 - 0.1390i

F =

0.6976 - 0.1688i -0.3077 - 0.1095i

-0.2000 - 0.1846i 0.1059 + 0.1243i

G =

1.0000 - 0.0000i -0.0000

0.0000 1.0000 - 0.0000i

H =

1.0000 + 0.0000i -0.0000 - 0.0000i

0.0000 1.0000 - 0.0000i

I =

1 0

0 1

J =

1.0e+006 *

-0.1832 + 3.0056i -0.0000 - 0.0001i

-0.0000 - 0.0000i -0.0003 - 0.0002i

12. z =1-2i

conjz = conj(z)

x = 3 + 4i;

realz = real(x)

u = 3+4i;

imagz = imag(u)

hasil

z =

1.0000 - 2.0000i

conjz =

1.0000 + 2.0000i

realz =

3

imagz =

4

13. z= 3+4i;

absz = abs(z)

Hasil

absz =

5

17. A = [3*exp(pi/3*j) 6*cos(pi/6)+i*6*sin(pi/6);3+4i 4.23*exp(-i*pi/18)+9]

B = [5-9j 5*exp(pi/3*j+pi/5);(2-3j)^3.3 log(6-8j)]

C = det(A)

D = conj(A)

E = A^2

F = A.^B

G = A

H = A

I = [A*B]

J = [A;B]

K = I(1,:)

L = J(:,1)

M = eig(A)

Hasil

A =

1.5000 + 2.5981i 5.1962 + 3.0000i

3.0000 + 4.0000i 13.1657 - 0.7345i

B =

5.0000 - 9.0000i 4.6861 + 8.1166i

-68.5109 + 6.9866i 2.3026 - 0.9273i

C =

18.0685 + 3.3192i

D =

1.5000 - 2.5981i 5.1962 - 3.0000i

3.0000 - 4.0000i 13.1657 + 0.7345i

E =

1.0e+002 *

-0.0091 + 0.3758i 0.7061 + 0.5368i

0.3654 + 0.6425i 1.7639 + 0.1044i

F =

1.0e+006 *

-0.1832 + 3.0056i -0.0000 - 0.0001i

-0.0000 - 0.0000i -0.0003 - 0.0002i

G =

1.5000 + 2.5981i 5.1962 + 3.0000i

3.0000 + 4.0000i 13.1657 - 0.7345i

H =

1.5000 + 2.5981i 5.1962 + 3.0000i

3.0000 + 4.0000i 13.1657 - 0.7345i

I =

1.0e+002 *

-3.4607 - 1.6974i 0.0069 + 0.2644i

-8.4587 + 1.3531i 0.1123 + 0.2919i

J =

1.5000 + 2.5981i 5.1962 + 3.0000i

3.0000 + 4.0000i 13.1657 - 0.7345i

5.0000 - 9.0000i 4.6861 + 8.1166i

-68.5109 + 6.9866i 2.3026 - 0.9273i

K =

1.0e+002 *

-3.4607 - 1.6974i 0.0069 + 0.2644i

L =

1.5000 + 2.5981i

3.0000 + 4.0000i

5.0000 - 9.0000i

-68.5109 + 6.9866i

M =

1.3675 + 0.0646i

13.2983 + 1.7989i

19. z =1+3i;

compass(z)

Hasil

20. z1 =1+i;

z2 = -(1+i);

z = [z1 z2];

feather (z)

title (plot using feather (z)= (1+i)

xlabel (real);ylabel (imaginary)

Hasil

KESIMPULAN

Matlab adalah sistem interaktif dengan elemen dasar array yang merupakan basis datanya. Array tersebut tidak perlu dinyatakan khusus seperti di bahasa pemograman yang ada sekarang. Hal ini memungkinkan anda untuk memecahkan banyak masalah perhitungan teknik, khususnya yang melibatkan matriks dan vektor dengan waktu yang lebih singkat dari waktu yang dibutuhkan untuk menulis program dalam bahasa C atau Fortran.

Untuk memahami matlab, terlebih dahulu anda harus sudah paham mengenai matematika terutama operasi vektor dan matriks, karena operasi matriks merupakan inti utama dari matlab. Pada intinya matlab merupakan sekumpulan sintak-sintak yang dapat dipanggil dan dieksekusi. Fungsi-fungsi tersebut dibagi-bagi berdasarkan kegunaannya dapat digunakan, dimodifikasi dan disebarkan secara bebas untuk tujuan bukan komersial (nonprofit), dengan syarat tidak menghapus atau merubah atribut penulis dan pernyataan yang disertakan dalam setiap dokumen. Tidak diperbolehkan melakukan penulisan ulang, kecuali mendapatkan ijin terlebih dahulu dari IlmuKomputer yang dikelompokan didalam toolbox yang ada pada matlab.